This page summarizes the main steps that lead to the final version of the EB DMulti-MADS algorithm.

NB: for most of the cases, the most performing versions of the DMulti-Mads use a spreading strategy and a strict acceptation success strategy.

For the first version, the EB DMulti-MADS algorithm uses a Orthomads random polling strategy. It was not efficient enough.

From left to right, data profiles with $\tau \in \{10^{-2}, 5 \times 10^{-2}, 10^{-1}\}$.

The choice of the norm for the selection center does not really impact the performing.

The second version adds an ordering of the poll directions according to the last success directions. It does not really improve the performance against dms algorithm.

From left to right, data profiles with .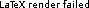

The third version uses a CS polling strategy (with ordering). It makes a huge impact on the performance. After discussion with Sebastien and Charles, this phaenomen is due to the fact that one third of the problems has separable variable objectives, and one third only one separable variable objective. The benchmark set is thus clearly biased in favor of coordinate search strategies. Infortunately, this benchmark set is considered as a standard even if it is crappy, and there is not enough good standard for multiobjective optimization. Put the blame on the reviewers of the DMS paper; but we have to deal with it.

From left to right, data profiles with .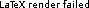

A speculative search strategy with a n+1 number of polling directions, which are sorted beat the DMS algorithm. This is what is proposed in the paper. It can be seen as an extension of the classical Mads strategy without models and heuristics.

Infortunately, the code used to process the data profiles has a bug. When fixed, the conclusions are quite different. Bimads for two objectives perform better, and DMulti-MADS is always ranked second, as it can be shown. The bug correction does not change the previous conclusions: use a spread strategy combined with a strict acceptance strategy is more efficient.

As suggested by Pierre-Yves, the hypervolume value is quite sensitive to the extent of the front. The idea consists in modifying the DMulti-Mads algorithm such that it focuses first on the extent of the front then on the densification of this last one. More precisely, the modification is the following: at each iteration, choose among the points with maximum mesh size parameter the ones which improve the extent of the current Pareto front approximation if they exist; if not, continue with the classical spreading strategy. Infortunately, the performance decreases as shown on these graphs for two objectives.

When comparing algorithms for two objectives and more, it comes as a surprise that average-nsgaii can be quite efficient on this set of problems.

Relaxing the constraint on the selection of the poll center gives a better performance. This is due to the fact that the algorithm can remained stuck around the same points until their mesh size parameters decrease significantly instead of exploring more potential interested parts of the objective space. The convergence analysis remains the same but needs to be refined a bit (still showing that the maximal mesh size parameter of the iterate list decrease.

For two objectives,

For two and more objectives,

When comparing the eight versions of DMulti-MADS with the relaxation, one can see that in this case, the dms versions are sligthly better (with better performance without opportunism); the use of spreading has a considerable impact on the performance. This version proposes an implementation which came close to the dms algorithm (but with better convergence analyzis). Practically, one can change the parameters such that having the same practical implementation of dms. Is it pertinent for publication ?

The behavior is similar when increasing the number of evaluations for two objectives with the original algorithm. For two objectives,

Similarly, changing the reference point for two objectives for the hypervolume indicator does not mess the results.

How close is the relaxation of the DMultimads algorithm to the DMS algorithm (with the no-strict criteria) ? The analysis below shows that using a threshold has an important impact on the performance of the algorithm (with the best parameters found until). No threshold (the algorithm selects only points with the maximum frame size/mesh size parameter, index 0) and the performance of the algorithm lags, what was observed before. Too big (similar to the DMS algorithm) (after 10) and one can see that the performance decreases. The best performance is reached for a threshold of 3, which is different from the DMS algorithm, where any point from the iterate list can be chosen as the best candidate.

When considering the strict criteria, it is more difficult to see.